Legenda
Sensore di inclinazione:
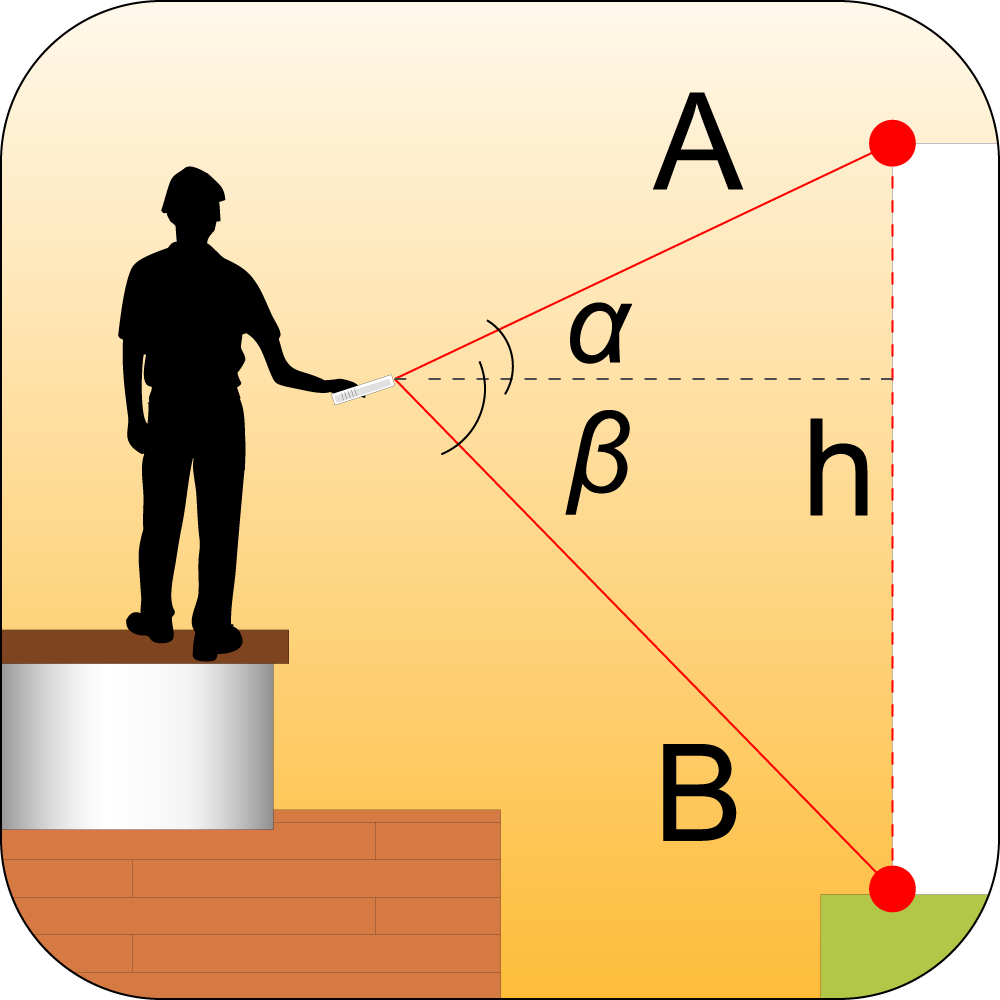
sostituisce e migliora le prestazioni della classica livella a bolla per mantenere lo strumento perfettamente orizzontale o verticale. Supporta la misurazione delle altezze parziali con applicazione della funzione Pitagora attraverso la rilevazione dell’angolo di inclinazione dello strumento rispetto alla linea orizzontale e l’applicazione automatica delle funzioni trigonometriche (h1= a x sin ά, h2 = b x sin β).
Funzione Pittore:
calcola l’area totale delle pareti e consente di stimare la quantità di materiale utile al lavoro. Somma automaticamente tutte le aree ottenute e le mostra per competenza.
Calcolo area triangolo e trapezio:
consente di dividere le stanze di forma complessa (cerchio o poligono) in settori e calcolare le loro aree.
Funzione di tracciamento:
consente di segnare una serie di punti ad una distanza predefinita. Il display mostra la distanza dal punto di tracciamento successivo.
Timer:
consente, soprattutto nella misurazione delle grandi distanze, di annullare l’effetto negativo delle vibrazioni dovute alla pressione dei tasti e al fissaggio sul treppiede. Permette di posizionare il riflettore prima della misurazione.
Accelerometro 3D incorporato con funzione Point-to-Point:
per calcolare la lunghezza di un segmento tra due punti arbitrari nello spazio. > Fissare il telemetro sul treppiede. Lo strumento memorizzerà lo spazio in cui si trova garantendo misurazioni più precise. > Rilevare il punto A e il punto B. Lo strumento calcola automaticamente la distanza tra i due punti indipendentemente da diagonali, distanze, altezze o eventuali ostacoli.
Teorema di Pitagora per le misurazioni indirette:
L’applicazione del teorema di Pitagora consente di misurare il terzo lato di un triangolo rettangolo (cateto), misurando gli altri due (ipotenusa e primo cateto) e di misurare dal basso l’altezza di pareti e altri elementi verticali (finestre, balconi, ecc.).
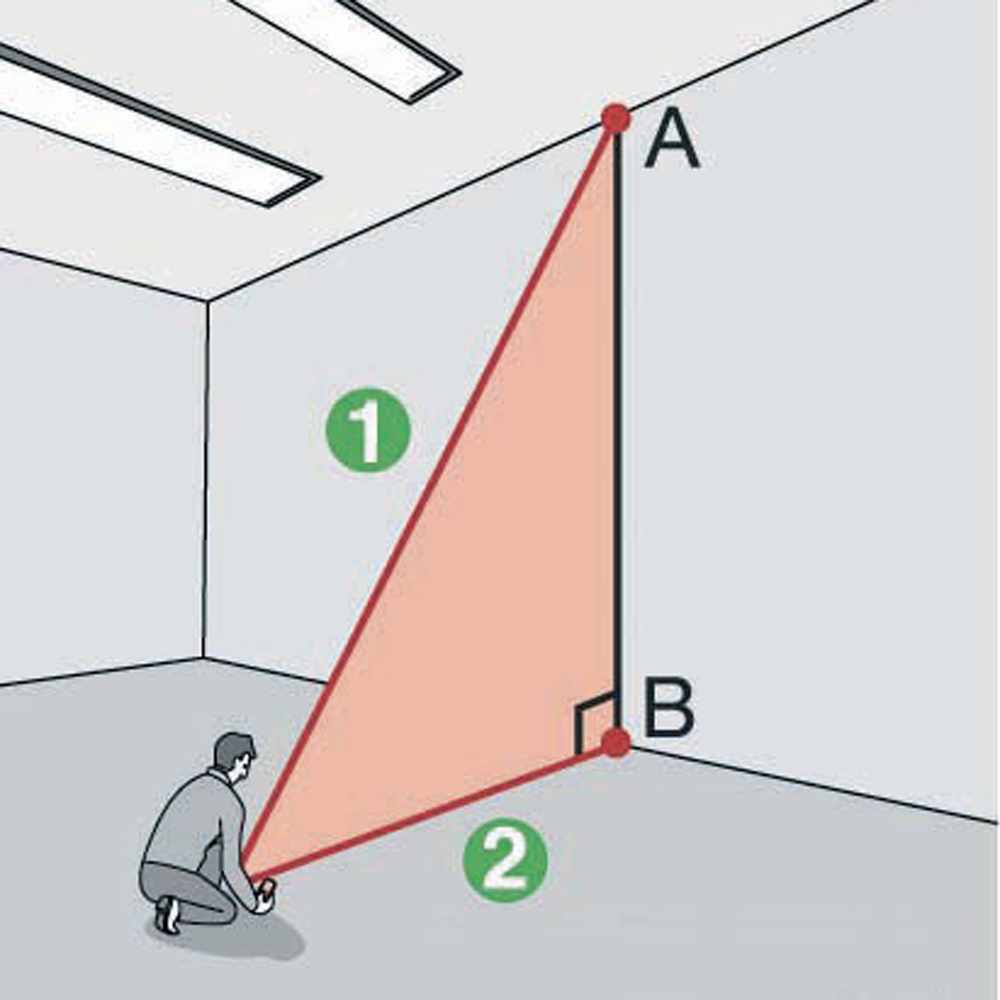
Teorema di Pitagora semplice - 2 punti:
per calcolare indirettamente le distanze orizzontali o verticali con due misure, la seconda perpendicolare al bersaglio.
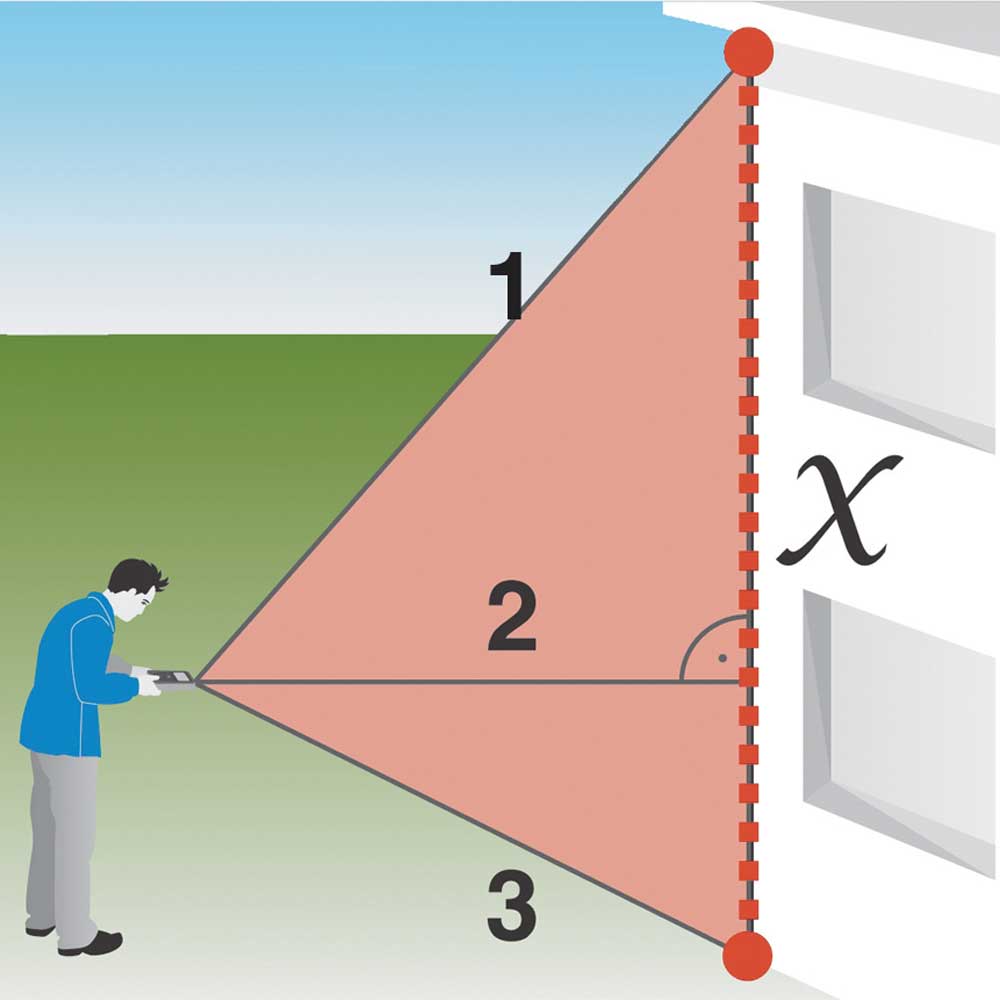
Teorema di Pitagora somma - 3 punti:
per calcolare il punto di misura giusto lungo la linea verticale anche in posizioni difficili o impossibili da raggiungere.
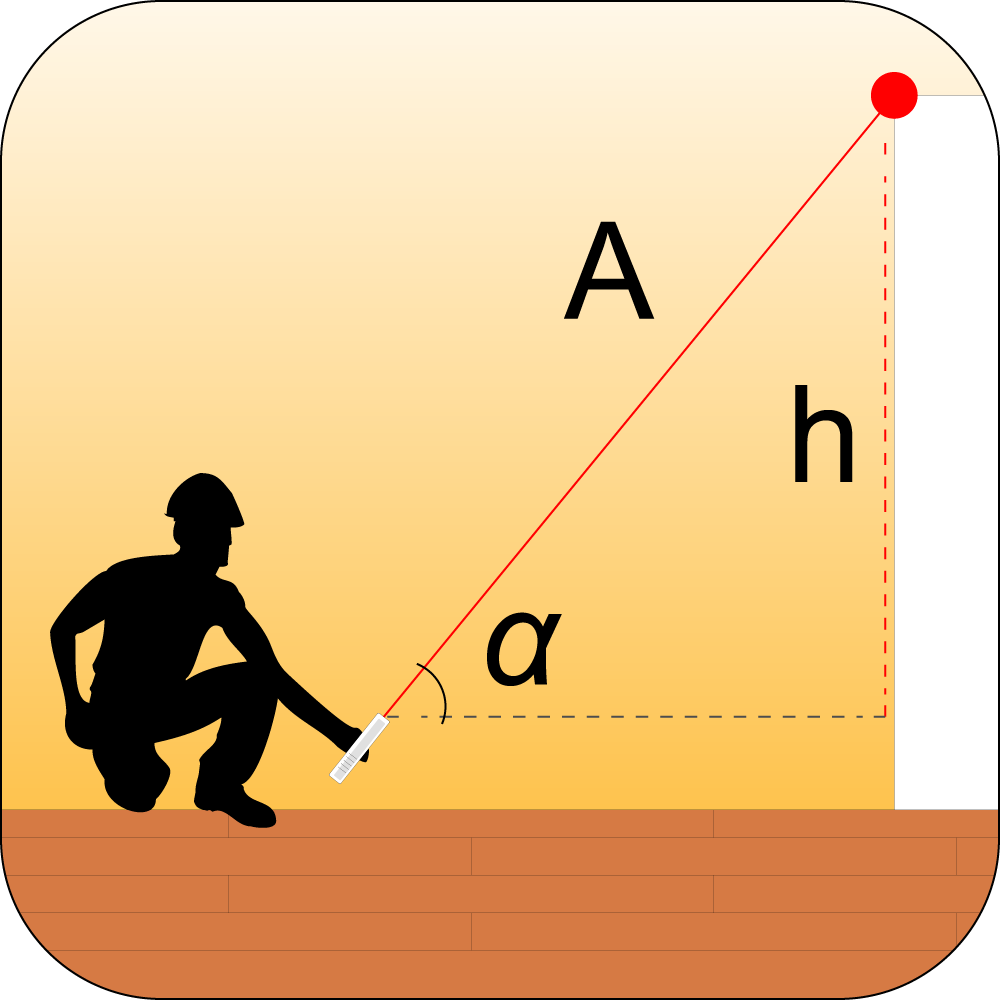
Teorema di Pitagora con sensore di inclinazione:
la presenza del sensore di inclinazione velocizza le misurazioni indirette riducendo, ad esempio nel teorema di Pitagora, le azioni in sequenza necessarie per completare l’operazione. Inoltre permette la misurazione di altezze anche in posizioni difficili o impossibili da raggiungere, come quella di una finestra o di un balcone lavorando da terra.